2

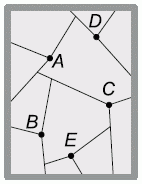
Крупный град поочередно пять раз попал в окно. В точках попадания — A, B, C, D и E — появились трещины, которые разошлись в стороны до столкновения с рамой или другими трещинами. В какой последовательности град попадал в окно?

A) DACBE       Б) ABCDE       В) BDACE       Г) BCDAE       Д) DCABE

3

У Василия есть 20 шариков разных цветов: жёлтые, зелёные, синие и чёрные. Из этих шариков ровно 17 не зелёные, 15 не чёрные и 12 не жёлтые. Сколько шариков являются синими?

A) 8       Б) 7       В) 6       Г) 4       Д) 3

4

В каком интервале находится значение 88 ∙ 888?

A) между 8 и 88

Б) между 88 и 888

В) между 888 и 8888

Г) между 8888 и 88888

Д) между 88888 и 888888

5

Какое число является квадратным корнем из 16¹⁶?

A) 4⁴       Б) 4⁸       В) 4¹⁶       Г) 8⁸       Д) 16⁴

6

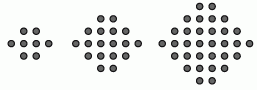
На рисунке изображены первые три фигуры последовательности. Сколько точек содержит пятая фигура этой последовательности?

A) 72       Б) 74       В) 76       Г) 78       Д) 80

7

Миша получил число x, разделив число √11 на 3. Где на числовой прямой находится число x?

A) между 0 и 1

Б) между 1 и 2

В) между 2 и 3

Г) между 3 и 4

Д) между 4 и 5

8

Раньше любимые шоколадные батончики Светы продавались в упаковках по 5 штук. Теперь каждая упаковка содержит 4 батончика, но цена осталась прежней. На сколько процентов выросла стоимость одного батончика?

A) на 10%

Б) на 20%

В) на 25%

Г) на 30%

Д) на 50%

9

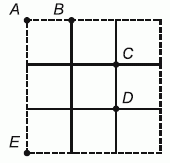
Роберт хочет выбрать четыре точки так, чтобы расстояния между всеми парами точек были разными. Какую из точек A, B, C, D и E необходимо убрать, чтобы это условие выполнялось?

A) A       Б) B       В) C       Г) D       Д) E

10

Рассмотрим единичный квадрат на координатной плоскости, заданный условиями

0 ≤ x ≤ 1 и 0 ≤ у ≤ 1.

Некоторые точки внутри этой области окрашены в чёрный цвет. Точка (x, у) окрашена в чёрный, если первая цифра после десятичной запятой в записи как x, так и у является нечётной. Как выглядит узор, образованный множеством точек (x, у)?

11

На координатной плоскости расположены четыре окружности радиусов r₁, r₂, r₃ и r₄, центры которых находятся в точках (0, 0), (1, 0), (3, 0) и (6, 0). Окружности не могут пересекаться, но могут касаться. Какое наибольшее значение может иметь сумма
r₁ + r₂ + r₃ + r₄?

A) 3

Б) 4

В) 5

Г) 6

Д) верхнего предела нет

12

Среди 10 различных положительных целых чисел ровно пять делятся на 5 и ровно семь делятся на 7. Пусть M — наибольшее из этих чисел. Чему равно наименьшее возможное значение M?

A) 105

Б) 77

В) 75

Г) 63

Д) другое значение

13

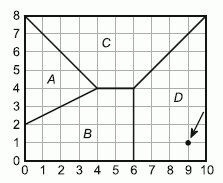
На рисунке изображена карта небольшого города с четырьмя школами. Территория города разделена на четыре региона A, B, C и D. Из всех точек каждого региона расстояние до своих школ меньше, чем до других школ. Известно, что школа в регионе D расположена в точке (9, 1). Определите координаты школы, находящейся в регионе A.

A) (0, 4)

Б) (1, 4)

В) (1, 5)

Г) (1, 6)

Д) (2, 4)

14

Чему равно наименьшее положительное целое число N, такое что 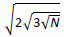является целым?

A) 2¹² ∙ 3⁶

Б) 2⁴ ∙ 3¹⁴

В) 2⁴ ∙ 3⁶ ∙ 5⁸

Г) 2⁴ ∙ 3²

Д) ни одно из перечисленных

15

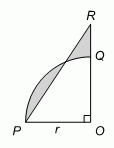
На рисунке изображены четверть круга OPQ и треугольник OPR. Две заштрихованные области имеют одинаковую площадь. Чему равна длина отрезка OR?

A) πr/2

Б) 3r/2

В) πr

Г) 2/π

Д) π/2r

16

На шахматной доске 4×4 расположены 16 кенгуру, по одному в клетке. За один ход каждый кенгуру перепрыгивает в соседнюю по стороне клетку. При этом все кенгуру остаются на доске, и в одной клетке может находиться несколько кенгуру. Какое максимальное количество пустых клеток может остаться после 100 ходов?

A) 15       Б) 14       В) 12       Г) 10       Д) 8

17

Пятизначное число N18NN делится на 18. Какое из следующих утверждений о цифре N верно?

A) существует ровно одно значение N

Б) существует ровно два значения N

В) существует ровно три значения N

Г) существует более трёх значений N

Д) не существует значений, которые N может принимать

18

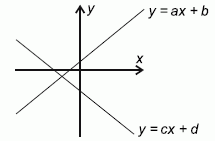
Ученик построил графики двух линейных функций, как показано на рисунке. Какое из следующих утверждений является верным для выражения
ab + cd − (ac + bd)?

A) Выражение отрицательно.

Б) Выражение неположительно.

В) Выражение положительно.

Г) Выражение равно нулю.

Д) Ни одно из вышеперечисленных утверждений не является верным.

19

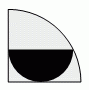
Площадь чёрного полукруга на рисунке равна 12 см². Чему равна площадь четверти большого круга?

A) 42 см²       Б) 36 см²       В) 32 см²       Г) 30 см²       Д) 25 см²

20

Когда бабушка начала вязать шерстяные носки, диаметр клубка пряжи составлял 30 см. После того, как она связала 70 носков, диаметр клубка стал равен 15 см. Сколько ещё носков бабушка сможет связать из оставшейся пряжи?

A) 70       Б) 50       В) 30       Г) 20       Д) 10

21

Ученик записал на доске два числа: 3 и 5. Затем он стёр их и вместо них записал их сумму и модуль разности. Этот процесс с полученными числами был повторён 50 раз. Какие два числа оказались на доске в итоге?

A) 3²⁵ и 5²⁵

Б) 3⁵⁰ и 5⁵⁰

В) 2 • 3²⁵ и 2 • 5²⁵

Г) 3 • 2²⁵ и 5 • 2²⁵

Д) ни один из вариантов

22

Иван выбрал произвольное двузначное число и записал его на доске. Затем он стёр его последнюю цифру. В результате число уменьшилось на p%. Какое из следующих чисел наиболее близко к максимальному возможному значению p?

A) 10       Б) 50       В) 90       Г) 95       Д) 99

23

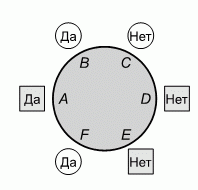
За круглым столом, как показано на рисунке, сидят три квадратных инопланетянина с Марса и три круглых инопланетянина с Юпитера. Один из них забрал ключ от летающей тарелки. Известно, что одна из групп (либо марсиане, либо юпитериане) всегда говорит правду, а другая — всегда лжёт. Каждому инопланетянину задали вопрос: «Есть ли у кого-то из сидящих рядом с вами ключ?» Их ответы представлены на рисунке. Определите, кто именно забрал ключ.

A) A       Б) B       В) C       Г) D       Д) E

24

Юля и её младшая сестра Полина отправились на велосипедную прогулку. Юля ехала с постоянной скоростью 18 км/ч, а Полина — 12 км/ч. Через 20 минут Юля устала и решила вернуться домой. На обратном пути она встретила Полину и сказала ей тоже возвращаться. Обе продолжили движение со своими прежними скоростями. На сколько минут позже Юли вернётся домой Полина?

A) 4       Б) 6       В) 8       Г) 10       Д) 15

25

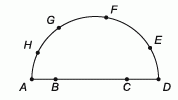
Точки B и C расположены на диаметре AD полуокружности, а точки E, F, G и H — на дуге полуокружности. Сколько различных треугольников c вершинами в точках A, B, C, D, E, F, G, H можно построить?

A) 15       Б) 50       В) 51       Г) 52       Д) 54

26

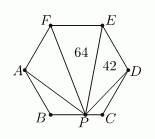
На рисунке изображён правильный шестиугольник ABCDEF. Точка P расположена на отрезке BC таким образом, что площадь △PEF равна 64, а площадь △PDE равна 42. Найдите площадь △APF.

A) 53       Б) 54       В) 56       Г) 60       Д) 64

27

На столе стоят три коробки, каждая из которых содержит три мяча – чёрные или белые. На коробках есть надписи, но они перепутаны так, что ни одна не соответствует реальному содержимому. Мы можем выбрать любую коробку, достать из неё мяч наугад, записать его цвет и не класть обратно. Какое наименьшее количество мячей нужно вытащить, чтобы точно определить состав каждой коробки?

A) 0       Б) 1       В) 2       Г) 3       Д) 4

28

На рисунке изображён правильный восьмиугольник со стороной 1 см. Из каждой его вершины проведена дуга окружности радиусом 1 см. Чему равен периметр серой области?

A) π см

Б) 2π/3 см

В) 8π/9 см

Г) 4π/5 см

Д) 3π/4 см

29

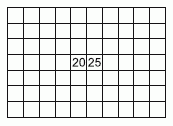
Патриция заполнила числами все клетки таблицы 7 × 10. Известно, что сумма всех чисел в любом прямоугольнике размером 3 × 4 или 4 × 3 равна нулю. На рисунке показаны значения в двух клетках. Чему равна сумма всех чисел в таблице?

A) −5

Б) −20

В) −25

Г) −45

Д) нельзя вычислить

30

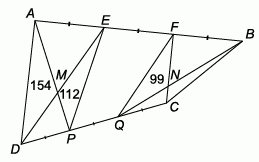
В выпуклом четырёхугольнике ABCD стороны AB и CD разделены на три части точками E, F, P и Q таким образом, что AE = EF = FB и DP = PQ = QC. Диагонали AEPD и FBCQ пересекаются в точках M и N соответственно. Площади треугольников AMD, EMP и FNQ равны 154, 112 и 99 соответственно. Чему равна площадь треугольника BCN?

A) 57       Б) 70       В) 72       Г) 86       Д) 141